来源:终结B站没人能讲清楚红黑树的历史,不服等你来踢馆!-【码炫课堂收费课节选之-红黑树源码解析及手写红黑树】
网友的总结:https://blog.csdn.net/weixin_44765605/article/details/117909521
一、前言
红黑树是数据结构中比较复杂的一种,找遍b站几平没有人能讲清楚,看着了很多所谓牛逼的大佬的课程,几平上来就是红黑树5大性质一去,再搞个旋转动图,然后开始讲节点插入操作,貌似以很牛逼,但是我从没着见几个讲节点删除操作的,更别谈能讲的透彻明白的,而且就插入节点这种情况而言,它是红黑树操作中相对简单点的,一般照着给定的规则也能看懂源码,但是很多人今天听了貌似懂了,但是明天就忘记了。
这就很奇怪了,不是听懂了吗?怎么还忘记了?说到底就是讲的人没讲明日,让你死硬背看色、旋转规则(其实连他自己都不知道为什么要定这样的规则),那听的人自然也就没听明日了,学红黑树不是学语文,靠死记硬背规则。所以那些误人子弟的垃圾讲师他只是告诉你红黑树的变色规和旋转规则,根本讲不出来为什么要变色?为什么要旋转?说到底就是因为他自已也不会,所以讲不出来,只会照本宣科,接照规则给你讲一遍,让你价们记任规则就行了,这样的结果肯定就是今天听了明天保证忘记。
smart哥决定把TreeMap的源码免费给大家手撕一遍(TreeMap完全是红黑树实现的,是由Josh Bloch 和 Doug Lea两位并发领域的大师共同完成的这个源码,整个TreeMap源码3000多行,代码量不大,但是TreeMap的红黑树的代码实现比红黑树发明者用到的算法更优越https://www.cs.usfca.edu/~galles/visualization/RedBlack.html 这个国外大学的网站上大家可以自己动手操作,大家可以看下删除操作它是找的前驱节点替代原删除节点,而TreeMap源码里面Doug Lea他们用的是后继节点替代原删除节点,这两种方案实际操作效果是一样的,只不过树的结构不一样,但是对应的红黑树都是平衡的,这个我会在视频讲解中演示,所以大家不要觉得奇怪为什么不一样),后面我还会免费给大家详细的讲解红黑树原理及源码。
学习本课程你将会收获如下:
- 5大性质的缘由,我会讲解为什么要有这5大性质
- 网络上红黑树的理解方式较为单一,一般是双黑、caseN法,而插入和删除的情况很多,每种都有对应的处理方式,如果死记硬背的话,再过一段时间再回忆各种情况可能就一头雾水了(
我会教你一种方法不用去死记硬背,保证能够立马记住)。 - Smar哥会讲解插入和删除的每一种情沉况并给出解释为什么要这么做,解释为任么要定义这样的规则(这里是关键,网上的课程基本都不会讲为什么变色?为什么要旋转?所以让你死记硬背规则,那么后果就是今天记得明天忘记,那么说到底也不能怪他们,因为他们自己也不会,所以只有糊弄小白了)
网络上讲红黑树的实现多来源于《算法导论》一书,直接讲红黑树的实现,需要处理颜色和高度两种属性约束,比较嗨涩。本文通过红黑树的等同——2-3-4树,避开颜色属性约束,也弱化了高度的影响,以另一种方式去理解红黑树,虽然并不能完全降低它的复杂度,但这种方式更易理解。
二、二叉查找树(BST)
定义
树:树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
树的基本术语:
- 节点的度:节点拥有的子树的数目。
- 叶子:度为零的节点。
- 分支节点:度不为零的节点。
- 树的度:树中节点的最大的度。
- 层次:根节点的层次为1,其余节点的层次等于该节点的双亲节点加1。
- 树的高度:树中节点的最大层次。
- 无序数:如果树中节点的各子树之间的次序是不重要的,可以交换位置。
- 有序数:如果树中结点的各子树的次序是重要的,不可以交换位置。
- 森林:0个或多个不相交的树组成。对森林加上一个跟,森林即成为树;删去跟,树即成为森林。
二叉树(Binary Tree):是一种常见的树状数据结构,它由一组节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;活着左、右子树皆为空。
完美二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth. All internal nodes have degree 2.
完全二叉树:完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。
A Complete Binary Tree (CBT) is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
完满二叉树:除了叶子结点之外的每一个结点都有两个孩子结点。
Every node except the leaf nodes have two children.
二叉查找树(二叉搜索树):就是一颗有序二叉树,它的左节点比父节点要小,右节点比父节点要大。它的高度决定的查找效率。
常见操作
查找(红黑树通用):查找每个节点时从根节点开始查找
- 查找值比当前值大,则搜索右子树
- 查找值等于当前值,停止查找,返回当前节点
- 查找值比当前值小,则搜索左子树
插入:要插入节点,必须先找到插入节点位置。依然是从根节点开始比较,小于根节点的话就和左子树比较,反之与右子树比较,直到左子树为空或者右子树为空,则插入到相应为空的位置。
遍历(红黑树通用):根据一定顺序来访问整个树,常见的有前序遍历、中序遍历(用的较多)、后序遍历。
特别形象:https://blog.csdn.net/weixin_44032878/article/details/88070556
- 前序遍历:根节点-》左子树-》右子树
中序遍历:左子树-》根节点-》右子树- 后续遍历:左子树-》右子树-》根节点
查找最小值(红黑树通用):沿着根节点的左子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最小节点。
查找最大值(红黑树通用):沿着根节点的右子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最大节点。
查找前驱节点(红黑树通用):小于当前节点的最大值。
查找后继节点(红黑树通用):大于当前节点的最小值。
删除:本质上是找前驱或者后继节点来替代被删除的节点。
- 叶子节点直接删除(没有前驱或后继节点)
- 只有一个子节点的用子节点替代(本质上就是找的前驱节点或者是后继节点,左节点就是前驱节点,右节点就是后继节点)
- 有两个子节点的,需要找到替代节点(替代节点就是前驱节点或者后继节点)
删除操作和红黑树一样,只不过红黑树多了着色和旋转过程。
三、BST存在的问题
BST存在的问题是,树在插入的时候会导致倾斜,不同的插入顺序会导致数的高度不一样,而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上,这样树的高度为N。
基于BST存在的问题,平衡查找二叉树(Balanced BST)产生了。平衡树的插入和删除的时候,会通过旋转操作将高度保持在LOgN。其中两款具有代表性的平衡树分别为AVL树(高度平衡树,具备二叉搜索树的全部特性,而且左右子树高度差不超过1)和红黑树。
AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写,他们提出的平衡二叉树的概念,为了纪念他们,将平衡二叉树 称为 AVL树。
AVL树本质上是一颗二叉查找树,但是它又具有以下特点:
- 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1。
- 左右两个子树 也都是一棵平衡二叉树。
AVL树如何实现平衡的?
通过左旋或者右旋(左旋右旋后一定不会破坏二叉搜索树的查找规则)
面试题:有了AVL树为什么还要红黑树呢?
AVL树由于实现比较复杂,而且插入和删除性能差(为什么?),在实际环境下的应用不如红黑树。
红黑树的实际应用非常广泛,如Java中的HashMap和TreeSet,Java8中HashMap的实现因为用RBTree代替链表(链表长度>8时),性能有所提升。
四、2-3-4树
定义
2-3-4树是四阶的B树(Balance Tree),它属于一种多路查找树,它的结构有以下限制:
- 所有叶子节点都拥有相同的深度。
- 节点只能是2-节点、3-节点、4-节点之一。
- 2-节点:包含1个元素的节点,有2个子节点;
- 3-节点:包含2个元素的节点,有3个子节点;
- 4-节点:包含3个元素的节点,有4个子节点;
- 所有节点必须至少包含1个元素
- 元素始终保持排序顺序,整体上保持二叉查找树的性质,即父节点大于左子节点,小于右子节点:而且节点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下图是一个典型的2-3-4树(来自维基百科):

2-3-4树的查询操作像普通的二叉搜索树一样,非常简单,但由于其结点元素数不确定,在一些编程语言中实现起来并不方便,实现一般使用它的等同——红黑树。
对应红黑树
就跟玩魔方一样,先给你一个结果(清一色6个面),然后你给我转,只要最后达到这个自的就行,那中间的步骤每个人都不一样,但是最后都达到了6个面,不同面都是不同的清一色。
至于为什么说红黑树是2-3-4树的一种等同呢,这是因为2-3-4树的每一个结点都对应红黑树的一种结构,所以每一棵2-3-4树也都对应一棵红黑树,下图是2-3-4树不同结点与红黑树子树的对应。
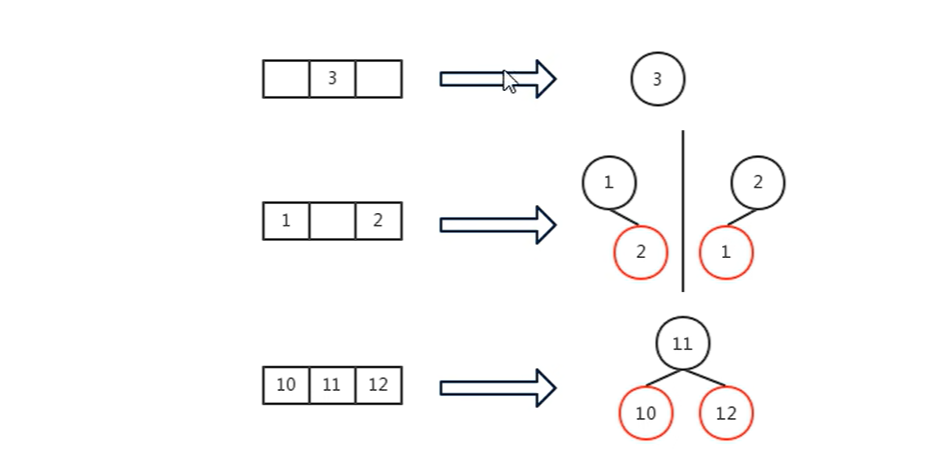
而上文中的2-3-4树也可以转换成一棵红黑树:
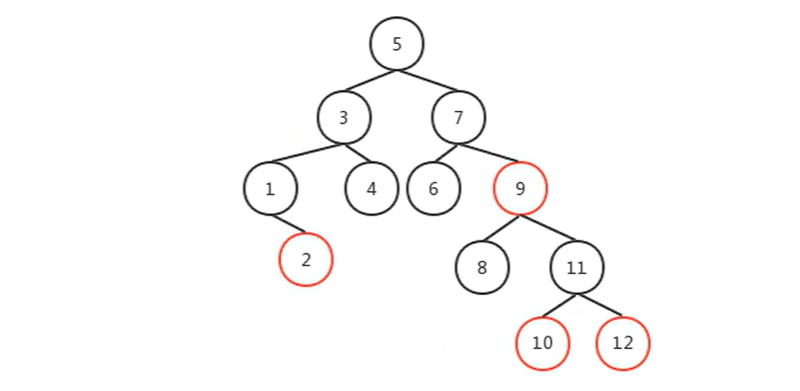
由红黑树的性质5,和2-3-4树的性质1,为了便于理解红黑树和2-3-4树的对应关系,我们可以把红黑树从根结点到叶子结点的黑色结点个数定义为高度。
红黑树和2-3-4树的结点添加和删除都有一个基本规则:避免子树高度变化,因为无论是2-3-4树还是红黑树,一旦子树高度有变动,势必会影其他子树进行调整,所以在插入和删除结点时尽量通过子树内部调整采达到平衡,2-3-4树实现平衡是通过结点的旋转和结点元素数变化,红黑树是通过结点旋转和变色。
下面对照着2-3-4树说一下红黑树结点的添加和删除:
结点插入
2-3-4树中结点添加需要遵守以下规则:
- 插入都是向最下面一层插入;
- 升元:将插入结点由2-结点升级成3-结点,或由3-结点升级成4-结点;
- 向4-结点插入元素后,需要将中间元素提到父结点升元,原结点变成两个2-结点,再把元素插入2-结点中,如果父结点也是4-结点,则递归向上层升元,至到根结点后将树高加1;
而将这些规则对应到红黑树里,就是:
- 新插入的结点颜色为红色,这样才可能不会对红黑树的高度产生影响。
- 2-结点对应红黑树中的单个黑色结点,插入时直接成功(对应2-结点升元)。
- 3-结点对应红黑树中的
黑+红子树,插入后将其修复成红+黑+红子树(对应3-结点升元); - 4-结点对应红黑树中的
红+黑+红子树,插入后将其修复成红色祖父+黑色父叔+红色孩子子树,然后再把祖父结点当成新插入的红色结点递归向上层修复,直至修复成功或遇到root结点;
公式:红黑树+新增一个节点(红色)=对等的2-3-4树+新增一个节点。
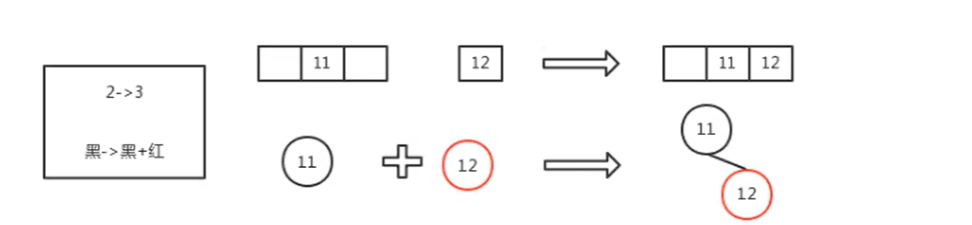
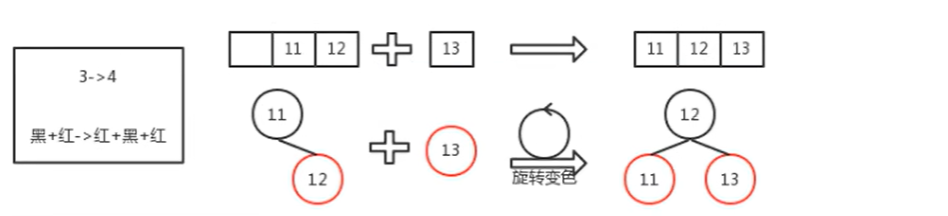
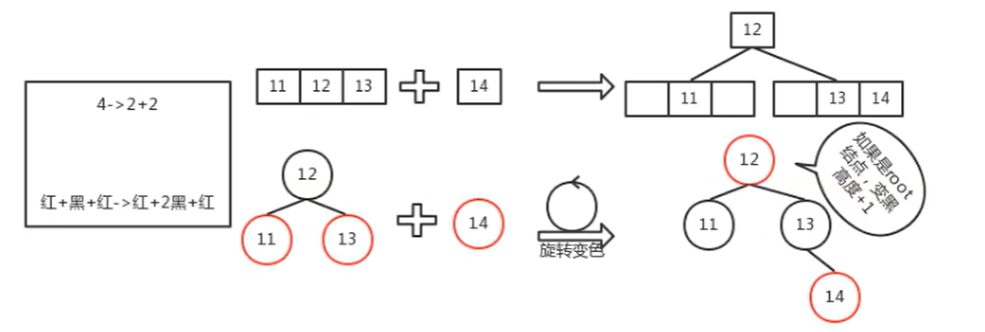
如上图所示,虽然向红黑树中插入了一个新结点,但由于旋转和变色,子树的高度保持不变。
练习(一个长序列生产2-3-4树)
删除结点
五、红黑树
定义
红黑树是一种结点带有颜色属性的二叉查找树,但它在二叉查找树之外,还有以下5大性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点,这类节点不可以忽视,否则代码会看不懂)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(黑色平衡)。
下图就是一个典型的红黑树:
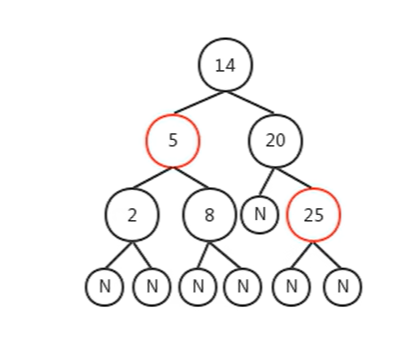
但实现上我省略了其中的Nil结点,一般如下图,大家理解时也可以忽略它们。
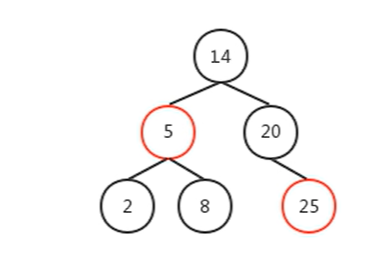
5大性质的解释推理
- 节点是红色或黑色。为什么?
- 答:任何节点在被添加到树中时是红色的,在转换和变色过程中可能会变成黑色。总共就红黑两种颜色。
- 根是黑色。为什么?
- 答:2-3-4树中,2-节点、3-节点、4-节点对应的红黑树的根节点都是黑色。
- 所有叶子都是黑色(叶子是NIL节点,这类节点不可以忽视,否则代码会看不懂)。为什么?
- 答:叶子是NIL节点,不画出来的。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)为什么?
- 答:2-3-4树中,3-节点对应的红黑树有两种情况:上黑下红(左倾)和上黑下红(右倾),一定会有一个红色节点。4-节点对应的是上1黑下2红,也有一个红色节点。2-节点直接对应一个黑色节点。 3-节点下面若是2个2-节点,则直接是两个黑色的子节点;若3-节点下面是2个3-节点,作为子树的3-节点一定是上黑下红,所以3-节点的红色节点下面一定连着两个黑色节点。若3-节点的子节点是2个4-节点,4-节点是上1黑下2红,则3-节点的红色节点下面也连着两个黑色节点。
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(黑色平衡)。为什么?
- 答:2-3-4树中,每个叶子节点(包括2-节点、3-节点、4-节点)到树根路径的层数是相同的,而每个路径经过的节点中均有1个黑色节点。
常见操作
- 变色:节点的颜色由黑变红或者由红变黑。
- 左旋:以某个节点作为旋转点,其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点,左子节点保持不变。
- 见动态图 todo
- 右旋:以某个节点作为旋转点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变。
- 见动态图 todo
- 新增:分情况讨论,主要是要找到插入位置,然后自平衡(左旋或者右旋)且插入节点是红色(如果是黑色的话,那么当前分支上就会多出一个黑色节点出来,从而破坏了黑色平衡),以下分析全部以左子树为例子,右子树的情况则相反。
- 如果插入的是第一个节点(根节点),红色变黑色
- 如果父节点为黑色,则直接插入,不需要变色
- 如果父节点为红色,叔叔节点也是红色(此种情况爷爷节点一定是黑色),则父节点和叔叔节点变黑色,爷爷节点变红色(如果爷爷节点是根节点,则再变成黑色),爷爷节点此时需要递归(把爷爷节点当做新插入的节点再次进行比较)
- 如果父节点是红色,没有叔叔节点或者叔叔节点是黑色(此时只能是NIL节点),则以爷爷节点为支点右旋,旋转之后原来的爷爷节点变红色,原来的父节点变黑色。
右子树的情况和左子树类似,请自行研究,不再整述。
- 删除(重点):通俗点讲就是三句话:自己能搞定的自己搞定;搞不定的找兄弟和父亲帮忙;父亲和兄弟都帮不了那有福同享,有难同当(父亲和兄弟自损)。
- 自己能搞定的自己搞定
- 如果删除的节点对应于2-3-4树的3节点或者4节点,则直接删除,不用跟兄弟和父亲借。
- 如果删除的是红色节点,则直接删;如果删除的是黑色节点,则红色节点上来替代,变黑即可。
- 搞不定的找兄弟和父亲帮忙
- 前提是找到“真正“的兄弟节点(如何找见视频讲解)
- 兄弟节点有的借(此时兄弟节点一定是黑色,如果是红色那说明这个节点不是真正的兄弟节点,需要回到上一步找真正的元弟节点
- 兄弟节点有两个子节点的情况(2个子节点肯定是红色,如果是黑色的话相当于此时兄弟节点对应2-3-4树是2节点,不可能有多余的元素可以借),此时需要旋转变色(具体见视频讲解)
- 兄弟节点只有一个子节点的情况,此时需要旋转变色(具体见视频讲解)
- 兄弟和父亲节点帮不了忙,于是开始递归自损
- 前提是找到“真正的兄弟节点(如何找见视频讲解)
- 兄弟节点没有多余的元素可借(此时兄弟节点一定为黑色2节点),此时兄弟节点所在分支也要自损一个黑色节点以此达到黑色平衡,最快的方式就是兄弟节点直接变红(相当于就是减少一个黑色节点),此时以父节点为root的子树又达到了平衡(两边都比之前少一个黑色)。但是以祖父节点为root的树依然是不平衡的,此时需要递归处理,具体见视频讲解。
- 自己能搞定的自己搞定
删除操作:
- 删除叶子节点,直接删除
- 删除的节点有一个子节点,则用子节点来替代
- 删除的节点有两个子节点,此时需要找到被删除节点的前驱节点或后继节点
删除节点方案:
1、找到前驱节点,复制前驱节点的值给待删除节点,然后删除前驱节点。
2、找到后继节点,复制后继节点的值给待删除节点,然后删除后继节点。
被删除的前驱节点或后继节点只有两种情况:
1、是叶子节点
2、有一个节点的节点。
- 前驱节点的子节点一定在左。
- 后继节点的子节点一定在右。
红黑树上的删除节点,一定对应2-3-4树的叶子节点。
优势和用途
首先红黑树是不符合AVL树的平衡条件的,即每个节点的左子树和右子树的高度最多差1的二叉查找树。但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。所以红黑树的插入效率更高!
红黑树适用于需要综合考虑插入、删除和查找操作的场景。例如,在Java的TreeMap和TreeSet中就使用了红黑树,它们需要频繁地进行插入和删除操作的同时,也要保证高效的查找性能。在HashMap中,红黑树用于优化长链表的性能问题,确保即便在哈希碰撞较多的情况下也能保持较好的查找效率。
六、小结
红黑树是一种自平衡二叉搜索树,广泛应用于各种数据结构中,尤其是在哈希表的实现中用于优化长链表的性能问题。
最后编辑:张三 更新时间:2024-10-25 09:04
